题目内容
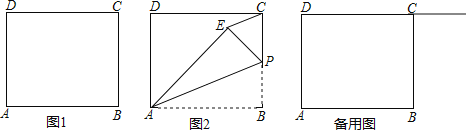
【题目】如图
，
是
的
边上的中点，过点的一条直线交
于
，交
的延长线于
，
交
于
，我们可以证明
成立（不要求考生证明）．
如图
，若将图中的过点的一条直线交于，改为交
的延长线于，交的延长线于，改为交于，其它条件不变，则还成立吗？如果成立，请给出证明；如果不成立，请说出理由；
根据图，请你找出
、
、
、
四条线段之间的关系，并给出证明；
如图
，若将图中的过点的一条直线交于，改为交的反向延长线于，交的延长线于，改为交于，其它条件不变，则得到的结论是否成立？
【答案】(1)成立,证明见解析;(2)见解析;
成立.
【解析】
（1）由于
，，那么本题要证得实际是
，因为
由此可得证．
（2）本题要根据两组相似三角形来求解，根据，得出
．可得出
．根据．可得出
．由于，将相等值进行替换即可得出
的比例关系．
（3）成立，和（2）的证法完全一样．
解：
成立．
证明：∵，
∴．
∴．
即
．
∵，
∴
．
．
证明：∵，
∴．
∴．
∵
，
∴
．
由，得．
∴
，即
．
成立，证明过程同
．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
