Question

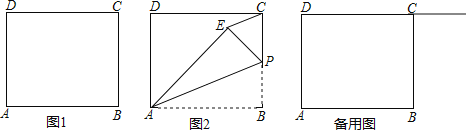
【题目】如图所示，矩形ABCD中，AB=12cm，AD=5cm，E是DC上一点（点E不与D、C重合）连接AE，以AE所在的直线为折痕，折叠纸片，点D的对应点为D′，点F为线段BC上一点，连接EF，以EF所在的直线为折痕折叠纸片，使点C的对应点C′落在直线ED′上，若CF=4时，DE=_____．

Answer 1

【答案】2或10

【解析】

设DE=x，则EC=12-x，然后证明△FEC∽△EAD，则，然后依据比例关系列出关于x的方程求解即可．

设DE=x，则EC=12-x．
由翻折的性质可知∠DEA=∠D′EA，∠CEF=∠C′EF，
∴∠AEF=90°．
∴∠DEA+∠CEF=90°．
又∵∠DAE+∠DEA=90°，
∴∠DAE=∠CEF．
又∵∠D=∠C=90°，
∴△FEC∽△EAD，

，即

解得x=2或x=10．
故答案是：2或10．