题目内容
【题目】已知,![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边作菱形
为边作菱形![]() ,使
,使![]() ,连接
,连接![]() .
.
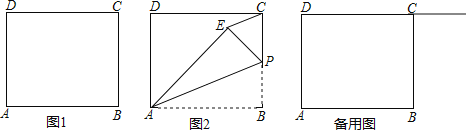
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 上时,
上时,
①求证:![]() ;②请直接判断结论
;②请直接判断结论![]() 是否成立;
是否成立;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,结论
的延长线上时,其他条件不变,结论![]() 是否成立?请写出
是否成立?请写出![]() 、
、![]() 、
、![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,且点
的延长线上时,且点![]() 、
、![]() 分别在直线
分别在直线![]() 的异侧,其他条件不变,请补全图形,并直接写出
的异侧,其他条件不变,请补全图形,并直接写出![]() 、
、![]() 、
、![]() 之间存在的等量关系.
之间存在的等量关系.

【答案】![]() ①证明见解析,②结论:
①证明见解析,②结论:![]() 成立;(2)结论
成立;(2)结论![]() 不成立.
不成立.![]() 、
、![]() 、
、![]() 之间的等量关系是
之间的等量关系是![]() .
.
![]() 补全图形如图见解析,
补全图形如图见解析,![]() 、
、![]() 、
、![]() 之间的等量关系是:
之间的等量关系是:![]() (或
(或![]() 以及这两个等式的正确变式).
以及这两个等式的正确变式).
【解析】
(1)此题只需由AB=AC,AD=AF,∠BAD=∠CAF,按照SAS判断两三角形全等得出∠ADB=∠AFC;
(2)此题应先判断得出正确的等量关系,然后再根据△ABD≌△ACF即可证明;
(3)此题只需补全图形后由图形即可得出∠AFC、∠ACB、∠DAC之间存在的等量关系.
解:![]() ①证明:∵
①证明:∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
在![]() 和
和![]() 中
中
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
②结论:![]() 成立.
成立.
![]() 结论
结论![]() 不成立.
不成立.
![]() 、
、![]() 、
、![]() 之间的等量关系是
之间的等量关系是![]() .
.
证明:∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 和
和![]() 中
中
![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
![]() 补全图形如下图:
补全图形如下图:

![]() 、
、![]() 、
、![]() 之间的等量关系是:
之间的等量关系是:![]()
(或![]() 以及这两个等式的正确变式).
以及这两个等式的正确变式).

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目