题目内容
5.一个半径为2cm的圆内接正六边形的面积等于6$\sqrt{3}$cm2.分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:如图所示:
设O是正六边形的中心,AB是正六边形的一边,OC是边心距,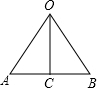
∠AOB=60°,OA=OB=2cm,
则△OAB是正三角形,
∴AB=OA=2cm,
OC=OA•sin∠A=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm),
∴S△OAB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$(cm2),
∴正六边形的面积=6×$\sqrt{3}$=6$\sqrt{3}$(cm2).
故答案为:6$\sqrt{3}$cm2.
点评 本题考查的正多边形和圆,理解正六边形被半径分成六个全等的等边三角形是解答此题的关键

练习册系列答案
相关题目
15.下列方程中属于一元一次方程的是( )
| A. | x-3y+3=0 | B. | x2-2x=3 | C. | x-2=1 | D. | $\frac{2}{x}$+x=1 |
16.若抛物线经过(0,1)、(-1,0)、(1,0)三点,则此抛物线的解析式为( )
| A. | y=x2+1 | B. | y=x2-1 | C. | y=-x2+1 | D. | y=-x2-1 |
15. 如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
 如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )| A. | SSS | B. | SAS | C. | AAS | D. | ASA |
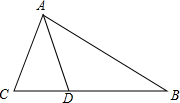 如图,△ABC中,∠BAC的角平分线交BC于D,且AB=AC+CD.
如图,△ABC中,∠BAC的角平分线交BC于D,且AB=AC+CD. 如图:在⊙O中,若∠ACB=30°,则∠AOB=60°.
如图:在⊙O中,若∠ACB=30°,则∠AOB=60°.