题目内容
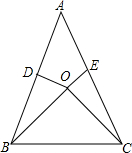 (1)如图,点O是△ABC内一点,OD⊥AB于D,OE⊥AC于E,且OB=OC,OD=OE,求证:△ABC是等腰三角形.
(1)如图,点O是△ABC内一点,OD⊥AB于D,OE⊥AC于E,且OB=OC,OD=OE,求证:△ABC是等腰三角形.(2)判断命题:“点O是△ABC所在平面内一点,OD⊥直线AB于D,OE⊥直线AC于E,且OB=OC,OD=OE,则△ABC是等腰三角形.”的真假,如果是命题请说明理由;若是假命题请举反例说明(画图说明)
考点:等腰三角形的判定,命题与定理
专题:
分析:(1)根据等边对等角得出∠OBC=∠OCB,然后根据三角形全等求得∠DBO=∠ECO,即可求得∠ABC=∠ACB,根据等角对等边即可证得结论;
(2)通过画图即可说明此命题是假命题.
(2)通过画图即可说明此命题是假命题.
解答:(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
在RT△ODB和RT△OEC中,
,
∴RT△ODB≌RT△OEC(HL),
∴∠DBO=∠ECO,
∴∠OBC+∠DBO=∠OCB+∠ECO,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
(2)是假命题;
如图所示,O是∠BAC的平分线与BC的垂直平分线的交点,
所以OB=OC,OD=OE,但△ABC不是等腰三角形.

∴∠OBC=∠OCB,
在RT△ODB和RT△OEC中,
|
∴RT△ODB≌RT△OEC(HL),
∴∠DBO=∠ECO,
∴∠OBC+∠DBO=∠OCB+∠ECO,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
(2)是假命题;
如图所示,O是∠BAC的平分线与BC的垂直平分线的交点,
所以OB=OC,OD=OE,但△ABC不是等腰三角形.

点评:本题考查了等腰三角形的判定和性质,三角形全等的判定和性质,以及命题的判定等,(2)举出反例是解题的关键.

练习册系列答案
相关题目
 如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )
如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=
| 2 |
| 11 |
| A、1个 | B、2个 | C、3个 | D、4个 |
某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计.下面5个判断中正确的有( )
①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④100名学生是总体的一个样本;⑤100名学生是样本容量.
①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④100名学生是总体的一个样本;⑤100名学生是样本容量.
| A、①② | B、①②④ |
| C、①③ | D、①③④⑤ |
已知点P在⊙O的内部,⊙O的半径为10cm,那么点P到⊙O的距离可以是( )
| A、9cm | B、10cm |
| C、11cm | D、12cm |

 △ABC在方格纸中的位置如图所示,方格纸中的每个小正方形的边长为1个单位,
△ABC在方格纸中的位置如图所示,方格纸中的每个小正方形的边长为1个单位,