题目内容
4．（1）先化简代数式$（{\frac{a+1}{a-1}+\frac{1}{{{a^2}-2a+1}}}）÷\frac{a}{a-1}$，然后选取一个使原式有意义的a的值代入求值．（2）解方程式：$\frac{x}{x+1}=\frac{2x}{3x+3}+1$．
分析 （1）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把a=2代入计算即可求出值；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=[$\frac{（a+1）（a-1）}{（a-1）^{2}}$+$\frac{1}{（a-1）^{2}}$]•$\frac{a-1}{a}$=$\frac{{a}^{2}}{（a-1）^{2}}$•$\frac{a-1}{a}$=$\frac{a}{a-1}$，
当a=2时，原式=2；
（2）去分母得：3x=2x+3x+3，
移项合并得：2x=-3，
解得：x=-1.5，
经检验x=-1.5是分式方程的解．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，已知等边三角形ABC边长为2，建立适当的平面直角坐标系，并写出各顶点的坐标．
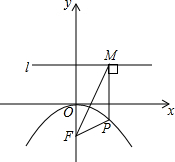如图，抛物线的顶点是原点，抛物线经过A点（8，-8），F点坐标为（0，-2），直线l为y=2，直线l平行于x轴．P点是抛物线上任意一点，过P点作PM⊥l，垂足为M点．
如图，E（-6，0），F（-4，-2），以O为位似中心按比例尺1：2把△EFO缩小到第一象限，则点F的对应点F′的坐标为（2，1）．