题目内容
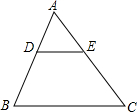如图，已知DE∥BC，AD=2，AB=5，则△ADE和△ABC的面积比是（ ）| A、2：3 | B、2：5 |
| C、4：9 | D、4：25 |
考点：相似三角形的判定与性质
专题：
分析：根据相似三角形的判定推出∠ADE∽△ABC，根据相似三角形的性质得出
=（
）2，代入求出即可．
| S△ADE |
| S△ABC |
| AD |
| AB |
解答：解：∵DE∥BC，
∴∠ADE∽△ABC，
∴
=（
）2，
∵AD=2，AB=5，
∴
=（
）2=
．
故选D．
∴∠ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
∵AD=2，AB=5，
∴
| S△ADE |
| S△ABC |
| 2 |
| 5 |
| 4 |
| 25 |
故选D．
点评：本题考查了相似三角形的性质和判定的应用，解此题的关键是能推出∠ADE∽△ABC，注意：相似三角形的面积比等于相似比的平方，难度适中．
练习册系列答案
相关题目
如图，∠A=15°，AB=BC=CD=DE=EF，则∠EDF等于（ ）| A、90° | B、75° |
| C、60° | D、45° |
如图，D是△ABC的边AC上的一点，若∠ABD=∠C，AB=6，AD=4，则线段CD的长为用配方法解方程x2-2x-5=0方程可变形为（ ）
| A、（x+1）2=4 |
| B、（x-1）2=4 |
| C、（x+1）2=6 |
| D、（x-1）2=6 |
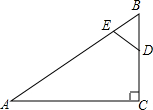如图，△ABC中，∠ACB=90°，AC=8cm，BC=6cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜15），连接DE，当△BDE是直角三角形时，t的值为