题目内容
18．关于x的方程$\frac{2x+5}{3}$=$\frac{5y+1}{4}$的解是非负数，则y的取值范围是多少？分析 首先解关于x的方程求得x的值，然后根据x是非负数得到关于y的不等式，求得y的范围．
解答 解：去分母，得4（2x+5）=3（5y+1），
则8x+20=15y+3，
即8x=15y-17，
解得：x=$\frac{15y-17}{8}$，
根据题意得：$\frac{15y-17}{8}$≥0，
解得：y≥$\frac{17}{5}$．
点评 本题是一个方程与不等式的综合题目．解关于x的不等式是本题的一个难点．
练习册系列答案
相关题目
6．-$\frac{\sqrt{3}}{2}$的绝对值是（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |
如图所示，点A，B，C．D的坐标分别为A（-3，0），B（0，6），C（0，1），D（2，0），试求直线AB与直线CD的交点坐标．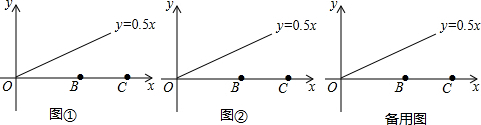
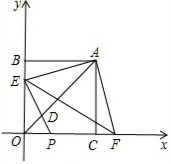在平面直角坐标系中，点A（m，m）在第一象限，且实数m满足条件：|$\sqrt{3}$-m|=m-$\sqrt{m-4}$，AB⊥y轴于B，AC⊥x轴于C