题目内容
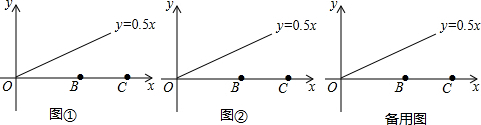
3.如图①,已知B(5,0),C(10,0)射线OP的解析式为y=0.5x.(1)射线OP上有一点M,使得S△MBC=7.5,求M点的坐标;
(2)如图②,在射线OP上有一点E,使得△OEB是等腰三角形,求E点的坐标.
分析 (1)求得BC=5,然后根据三角形的面积即可求得M的纵坐标,代入y=0.5x即可求得横坐标;
(2)分三种情况分别讨论即可求得.
解答 解:(1)∵B(5,0),C(10,0),
∴BC=10-5=5,
∵S△MBC=7.5,
∴$\frac{1}{2}$BC•yM=7.5,
∴yM=3,
代入y=0.5x得,3=0.5x,
∴x=6,
∴M(6,3);
(2)∵B(5,0),
∴OB=5,
①当OE=OB=5时,设E(x,0.5x),
根据勾股定理,得x2+(0.5x)2=52,
解得x=2$\sqrt{5}$,
∴E(2$\sqrt{5}$,$\sqrt{5}$);
②当OE=EB时,E的横坐标为2.5,
把x=2.5代入y=0.5x得,y=$\frac{5}{4}$,
∴E($\frac{5}{2}$,$\frac{5}{4}$);
③当OB=BE=5时,设E(x,0.5x),
根据勾股定理,得(x-5)2+(0.5x)2=52,
解得x=8,
∴E(8,4).
综上,在射线OP上有一点E,使得△OEB是等腰三角形的E的坐标为(2$\sqrt{5}$,$\sqrt{5}$)或($\frac{5}{2}$,$\frac{5}{4}$)或(8,4).
点评 本题考查了一次函数图象上点的坐标特征,等腰三角形的判定,分类讨论思想的运用是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列说法正确的是( )
| A. | 368精确到万位 | B. | 2.58精确到百分位 | ||
| C. | 0.0450精确到千分位 | D. | 1.48×103精确到百分位 |
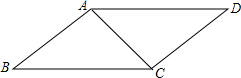 如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.
如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.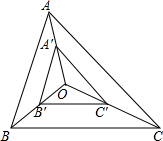 如图,O为△ABC内任意一点,点A′、B′、C′分别是线段OA,OB,OC的中点,△A′B′C′与△ABC相似吗?为什么?
如图,O为△ABC内任意一点,点A′、B′、C′分别是线段OA,OB,OC的中点,△A′B′C′与△ABC相似吗?为什么? 在△ABC中,D、E为AB、AC的中点,CD、BE相交于点O,M、N分别为OB、OC的中点,求证:DM∥EN.
在△ABC中,D、E为AB、AC的中点,CD、BE相交于点O,M、N分别为OB、OC的中点,求证:DM∥EN.