题目内容
9.已知多项式x2+(m+k)x+k可以分解因式为(x+2)(x+4),求m、k的值.分析 根据因式分解与整式的乘法互为逆运算,可得答案.
解答 解:(x+2)(x+4)=x2+6x+8=x2+(m+k)x+k,
$\left\{\begin{array}{l}{m+k=6}\\{k=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-2}\\{k=8}\end{array}\right.$.
点评 本题考查了因式分解的意义,利用整式的乘法与因式分解的关系得出方程组是解题关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.当x=-$\frac{1}{2}$时,下列各式的值为$\frac{3}{4}$的是( )
| A. | x2+x+1-2x2-x | B. | 2x2-x+1-x2+x | C. | $\frac{1}{2}$x2-2x+1-x2+x | D. | -x2-x+$\frac{1}{2}$x2+1 |
14.下列说法正确的是( )
| A. | 368精确到万位 | B. | 2.58精确到百分位 | ||
| C. | 0.0450精确到千分位 | D. | 1.48×103精确到百分位 |
 如图是一个数字转换机,写出图(1)的输出结果,图(2)的转换步骤.
如图是一个数字转换机,写出图(1)的输出结果,图(2)的转换步骤.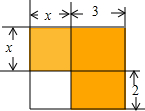 用整式填空,指出单项式的次数以及多项式的次数和项.
用整式填空,指出单项式的次数以及多项式的次数和项.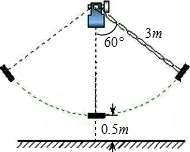 如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?