题目内容
9.要求:①A、B为整式;②A为被除式,B为除式,商必须为2xy.(1)若A=x3y-2xy2,则B=$\frac{1}{2}$x2-y;
(2)若B=x+y,则A=2x2y+2xy2;
(3)若A=3x2,则是否存在B?请说明理由.
分析 (1)利用被除数除以商,就可以求得B;
(2)根据被除式=除式×商求得被除式求解;
(3)利用被除式除以商,然后判断所得结果是否是整式即可判断.
解答 解:(1)B=(x3y-2xy2)÷2xy=$\frac{1}{2}$x2-y,
故答案是:$\frac{1}{2}$x2-y;
(2)A=(x+y)•2xy=2x2y+2xy2;
故答案是:2x2y+2xy2;
(3)B=3x2÷2xy=$\frac{3x}{y}$,不是整式,在B不存在.
点评 本题考查了整式的除法,理解被除式、除式和商之间的关系是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图是一个数字转换机,写出图(1)的输出结果,图(2)的转换步骤.
如图是一个数字转换机,写出图(1)的输出结果,图(2)的转换步骤.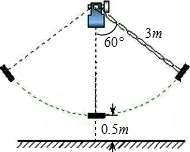 如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?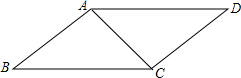 如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.
如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.