题目内容
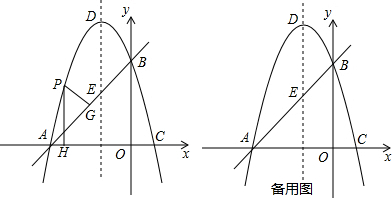
填空完成推理过程：如图，△ABC中，∠A=∠B，延长BC到D，作CE∥BA，试说明∠ACE=∠ECD．
解：∵CE∥BA（已知）
∴∠ACE=∠A
∵CE∥BA（已知）
∴∠B=
∵∠A=∠B（已知）
∴∠ACE=∠ECD．
考点：平行线的判定与性质
专题：推理填空题
分析：根据“两直线平行，内错角、同位角”相等和等量代换证得结论．
解答：解：∵CE∥BA（已知）
∴∠ACE=∠A （两直线平行，内错角相等）
∵CE∥BA（已知）
∴∠B=∠ECD（两直线平行，同位角相等）
∵∠A=∠B（已知）
∴∠ACE=∠ECD．
故答案是：（两直线平行，内错角相等）；∠ECD（两直线平行，同位角相等）．
∴∠ACE=∠A （两直线平行，内错角相等）
∵CE∥BA（已知）
∴∠B=∠ECD（两直线平行，同位角相等）
∵∠A=∠B（已知）
∴∠ACE=∠ECD．
故答案是：（两直线平行，内错角相等）；∠ECD（两直线平行，同位角相等）．
点评：本题考查了平行线的性质．平行线的性质是由平行关系来寻找角的数量关系．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若a＞b，则下列各式中不正确的是（ ）
| A、a-3＞b-3 | ||||
| B、-3a＜-3b | ||||
C、
| ||||
D、
|
已知有关于x，y整式（b-1）xay3+（b+1）y2与2x2y3的和为单项式，求a+b（ ）
| A、1 | B、0 | C、-1 | D、-2 |
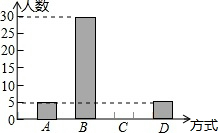八（3）班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班50名学生的处理方式进行统计，得出相关统计表和统计图（如图）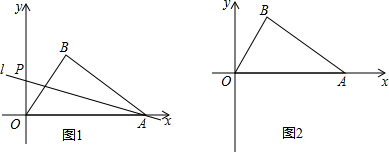
如图，△ABC中，A，B，C的坐标分别不（-2，1）（-1，-3），（-5，-1），把△ABC平移使点C移到原点O处，得到△A1B1O．