题目内容
1．
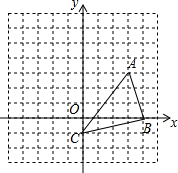如图，点A的坐标为（3，3），点B的坐标为（4，0），点C的坐标为（0，-1）．（1）请在直角坐标系中画出△ABC绕着点C逆时针旋转90°后的图形△A′B′C′；
（2）点A′的坐标为（-4，2），点B′的坐标为（-1，3）．
分析 （1）利用网格和旋转的性质画出点A、B的对应点A′和B′，从而得到△A′B′C′；
（2）根据所画图形写出A′和B′的坐标．
解答 解：（1）如图，△A′B′C′为所作；
（2）点A′的坐标为（-4，2），点B′的坐标为（-1，3）．
故答案为-4，2，-1，3．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
口算题天天练系列答案
相关题目
9．
已知三角形A₁B₁C₁是由三角形ABC经过平移得到的，它们各对应顶点在平面直角坐标系中的坐标如下表所示：
（1）观察表中各对应点坐标的变化，并填空：a=0，b=2，c=9；
（2）在平面直角坐标系中画出三角形ABC及三角形A₁B₁C₁．
已知三角形A₁B₁C₁是由三角形ABC经过平移得到的，它们各对应顶点在平面直角坐标系中的坐标如下表所示：| 三角形ABC | A（a，0 ） | B（3，0） | C（5，5） |
| 三角形A₁B₁C₁ | A₁（4，2） | B₁（7，b） | C₁（c，7） |
（2）在平面直角坐标系中画出三角形ABC及三角形A₁B₁C₁．
14．已知a3=2，b5=3，则a、b的大小关系是（ ）
| A． | a＜b | B． | a＞b | C． | a=b | D． | 不确定 |
如图，在四边形AOBC中，AC∥OB，顶点O是原点，顶点A的坐标为（0，8），AC=24cm，OB=26cm，点P从点A出发，以1cm/s的速度向点C运动，点Q从点B同时出发，以3m/s的速度向点O运动．规定其中一个动点到达端点时，另一个动点也随之停止运动；从运动开始，设P（Q）点运动的时间为ts．