题目内容
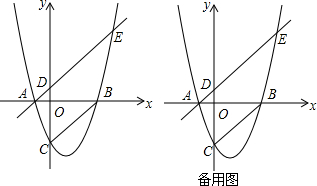
1.已知抛物线y=ax2+bx+c经过点P(6,8)及点P关于原点对称的点Q.(1)求证:该抛物线一定与x轴有两个不同的交点;
(2)设抛物线与x轴的两个交点为A,B,与y轴的交点为C,连接AC,BC,设∠CBA=α,∠CAB=β,是否满足tanα=tanβ的抛物线?如果存在,求出它的解析式,如果不存在,请说明理由.
分析 (1)求出点P关于原点对称的点Q的坐标,把点P、Q的坐标代入解析式,用a不是b、c,根据判别式判断抛物线与x轴的交点情况;
(2)根据tanα=tanβ,得到OA和OB的关系,进行判断即可.
解答 解:(1)点P关于原点对称的点Q的坐标为(-6,-8),
$\left\{\begin{array}{l}{36a+6b+c=8}\\{36a-6b+c=-8}\end{array}\right.$,
解得c=-36a,b=$\frac{4}{3}$,
∴解析式为:y=ax2+$\frac{4}{3}$x-36a,
△=$\frac{16}{9}$+144a2>0,
∴抛物线一定与x轴有两个不同的交点;
(2)∵tanα=tanβ,
∴OA=OB,
x1+x2=-$\frac{4}{3a}$=0,无解,
∴抛物线不存在.
点评 本题考查的是抛物线与x轴的交点的求法,掌握关于原点对称的点的坐标的关系和判别式是解题的关键,注意数形结合思想在解题中的运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
11.函数$y=\frac{x}{x-1}$中自变量x的取值范围是( )
| A. | x>1 | B. | x>0 | C. | x≠0 | D. | x≠1 |
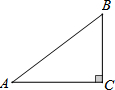 如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm
如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm