题目内容
6.解方程(组)(1)$\frac{x}{x-2}$-$\frac{2}{{x}^{2}-4}$=1.
(2)$\left\{\begin{array}{l}2x-y=3\\ 5x+y=11\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)去分母得:x2+2x-2=x2-4,
解得:x=-1,
经检验x=-1是分式方程的解;
(2)$\left\{\begin{array}{l}{2x-y=3①}\\{5x+y=11②}\end{array}\right.$,
①+②得:7x=14,即x=2,
把x=2代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
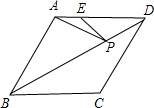 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.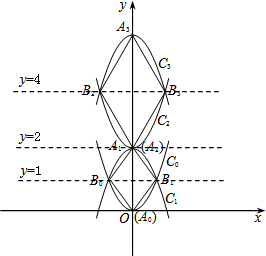 如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….
如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….