题目内容
2.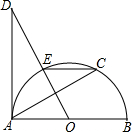 已知AB是半⊙O的直径,∠D=50°,AD切⊙O于点A,连接DO交半⊙O于点E,作EC∥AB交半⊙O于C点,连接AC,则∠CAB的度数为20°.
已知AB是半⊙O的直径,∠D=50°,AD切⊙O于点A,连接DO交半⊙O于点E,作EC∥AB交半⊙O于C点,连接AC,则∠CAB的度数为20°.
分析 根据切线的性质得AD⊥OA,则利用互余可计算出∠AOD=40°,再根据圆周角定理得到∠ECA=$\frac{1}{2}$∠AOE=20°,然后根据平行线的性质可得∠CAB的度数.
解答 解:∵AD切⊙O于点A,
∴AD⊥OA,
∴∠DAO=90°,
∴∠AOD=90°-∠D=90°-50°=40°,
∴∠ECA=$\frac{1}{2}$∠AOE=20°,
∵CE∥AB,
∴∠CAB=∠ECA=20°.
故答案为20°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.

练习册系列答案
相关题目
13.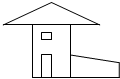 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )| A. | 三角形、长方形 | B. | 三角形、正方形、长方形 | ||
| C. | 三角形、正方形、长方形、梯形 | D. | 正方形、长方形、梯形 |
17.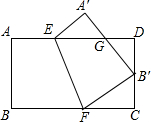 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )| A. | 9:4 | B. | 3:2 | C. | 16:9 | D. | 4:3 |
 如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是$\frac{1}{4}$,则大、小两个正方形的边长之比是2:1.
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是$\frac{1}{4}$,则大、小两个正方形的边长之比是2:1.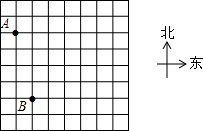 在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1)、(-2,-3),以及点C的坐标为(3,2)(单位:km).
在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1)、(-2,-3),以及点C的坐标为(3,2)(单位:km).