题目内容
16.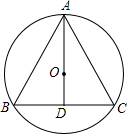 ⊙0外接等腰△ABC,AB=AC,连AO并延长BC与D,BC=12,cosB=$\frac{3}{5}$,求:半径长.
⊙0外接等腰△ABC,AB=AC,连AO并延长BC与D,BC=12,cosB=$\frac{3}{5}$,求:半径长.
分析 由AB=AC得出$\widehat{AB}$=$\widehat{AC}$,进而根据垂径定理得出AE⊥BC,BD=BC=$\frac{1}{2}$BC=6,解直角三角形求得AB,进而应用勾股定理求得AD,连接OB,设圆的半径为x,则OD=AD-OA=8-x,然后根据勾股定理即可求得.
解答 解:∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$
∴AE⊥BC,BD=BC=$\frac{1}{2}$BC=6,
∵cosB=$\frac{3}{5}$,
∴$\frac{BD}{AB}$=$\frac{3}{5}$,
∴AB=10,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
连接OB,设圆的半径为x,则OD=AD-OA=8-x,
在RT△BOD中,OB2=BD2+OD2,
即x2=62+(8-x)2,解得x=$\frac{25}{4}$
∴⊙0的半径为$\frac{25}{4}$.
点评 本题考查了垂径定理,勾股定理以及解直角三角形,熟练掌握性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.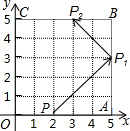 如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…第n次碰到正方形的边时的点为Pn,则P2015的坐标是( )
如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…第n次碰到正方形的边时的点为Pn,则P2015的坐标是( )
 如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…第n次碰到正方形的边时的点为Pn,则P2015的坐标是( )
如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…第n次碰到正方形的边时的点为Pn,则P2015的坐标是( )| A. | (5,3) | B. | (3,5) | C. | (0,2) | D. | (2,0) |
5.函数y=(1-x)2的自变量x的取值范围是( )
| A. | x≠1 | B. | x>0 | C. | x>1 | D. | 全体实数 |
 如图,在△ABC中,AD⊥BC于D,点M、N分别在BC所在的直线上,且AB=AC,BM=CN,试判断△AMN的形状,并说明理由.
如图,在△ABC中,AD⊥BC于D,点M、N分别在BC所在的直线上,且AB=AC,BM=CN,试判断△AMN的形状,并说明理由. 如图,A,B,C,D是⊙O上的点,且$\widehat{AC}=\widehat{BD}$.求证:AB∥CD.
如图,A,B,C,D是⊙O上的点,且$\widehat{AC}=\widehat{BD}$.求证:AB∥CD.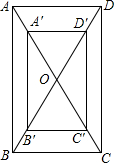 一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2.
一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2. 如图,数轴上有A,B两点,表示的数分别为a,b.已知(a+1)2与|b-3|互为相反数,点P为数轴上一动点(不与点A,B重合),其表示的数为x.
如图,数轴上有A,B两点,表示的数分别为a,b.已知(a+1)2与|b-3|互为相反数,点P为数轴上一动点(不与点A,B重合),其表示的数为x.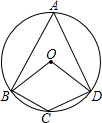 如图,四边形ABCD是⊙O的内接四边形,且OB∥DC,OD∥BC,则∠BOD=120°.
如图,四边形ABCD是⊙O的内接四边形,且OB∥DC,OD∥BC,则∠BOD=120°.