题目内容
已知平行四边形ABCD，∠A=60°，AB=2a，AD=a．请计算两条对角线的长度．考点：平行四边形的性质
专题：
分析：首先连接BD，AC，由∠A=60°，AB=2a，AD=a，利用余弦定理，即可求得BD的长，然后由勾股定理的逆定理，证得∠ADB=90°，再利用勾股定理求得OA的长，继而求得AC的长．
解答：
解：连接BD，AC，
∵∠DAB=60°，AB=2a，AD=a，
∴BD2=AB2+AD2-2AB•AD•cos∠DAB=4a2+a2-2×2a×a×
=3a2，
∴BD=
a，
∴AB2=BD2+AD2，
∴∠ADB=90°，
∵四边形ABCD是平行四边形，
∵OD=
BD=
a，
∴OA=
=
a，
∴AC=2OA=
a．
解：连接BD，AC，∵∠DAB=60°，AB=2a，AD=a，
∴BD2=AB2+AD2-2AB•AD•cos∠DAB=4a2+a2-2×2a×a×
| 1 |
| 2 |
∴BD=
| 3 |
∴AB2=BD2+AD2，
∴∠ADB=90°，
∵四边形ABCD是平行四边形，
∵OD=
| 1 |
| 2 |
| ||
| 2 |
∴OA=
| AD2+OD2 |
| ||
| 2 |
∴AC=2OA=
| 7 |
点评：此题考查了平行四边形的性质、余弦定理以及勾股定理等知识．此题难度较大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
小题狂做系列答案
相关题目
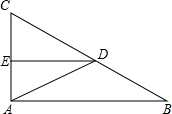如图所示，在△ABC中，∠BAC=90°，D为BC的中点，DE⊥AC于点E，∠ADB=2∠ADC，求∠ADE的度数．
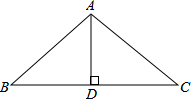如图，在△ABC中，∠BAC=108°，AB=AC，AD⊥BC，垂足为D，求∠BAD的度数．
如图，一次函数y=kx+b的图象与x轴的交点坐标为（2，0），则下列说法：①y随x的增大而减小；②b＞0；③关于x的方程kx+b的解为x=2；④kx+b＜0的解集是x＜2．其中说法正确的有