题目内容
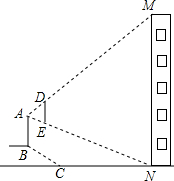 如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡长为8米,坡角恰好为30°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(结果精确到1米,
如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡长为8米,坡角恰好为30°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(结果精确到1米,| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:延长AB交CN于点F,根据斜坡长为8米,坡角恰好为30°,得到CF=4
米,从而得到FN=FC+CN=(20+4
)米,根据△ADE∽△AMN利用相似三角形的对应边的比相等得到MN的长即可.
| 3 |
| 3 |
解答: 解:如图,延长AB交CN于点F,
解:如图,延长AB交CN于点F,
∵斜坡长为8米,坡角恰好为30°,
∴CF=4
米,
∴FN=FC+CN=(20+4
)米,
∵△ADE∽△AMN,
∴
=
,
即:
=
,
解得:MN=44.88米.
答:这栋楼的高度为44.88米.
 解:如图,延长AB交CN于点F,
解:如图,延长AB交CN于点F,∵斜坡长为8米,坡角恰好为30°,
∴CF=4
| 3 |
∴FN=FC+CN=(20+4
| 3 |
∵△ADE∽△AMN,
∴
| AH |
| AG |
| DE |
| MN |
即:
| 0.6 | ||
20+4
|
| 1 |
| MN |
解得:MN=44.88米.
答:这栋楼的高度为44.88米.
点评:本题考查了坡度坡角问题,解题的关键是利用坡度的知识求得线段CF的长,从而求得线段FN的长.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
以直角三角形的三边为边长分别向外作正方形,已知其中两个正方形的面积分别为20和16,则第三个正方形的边长为( )
A、2
| ||
| B、4或6 | ||
C、2
| ||
| D、2或6 |
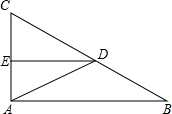 如图所示,在△ABC中,∠BAC=90°,D为BC的中点,DE⊥AC于点E,∠ADB=2∠ADC,求∠ADE的度数.
如图所示,在△ABC中,∠BAC=90°,D为BC的中点,DE⊥AC于点E,∠ADB=2∠ADC,求∠ADE的度数.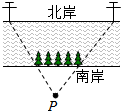 如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为
如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为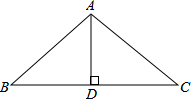 如图,在△ABC中,∠BAC=108°,AB=AC,AD⊥BC,垂足为D,求∠BAD的度数.
如图,在△ABC中,∠BAC=108°,AB=AC,AD⊥BC,垂足为D,求∠BAD的度数.