题目内容
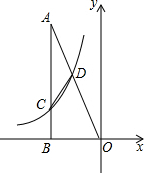 如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )
如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
考点:反比例函数系数k的几何意义
专题:
分析:过D作DE⊥AB于E,作DF⊥OB于F,得到OB=2DE和AB=
AC,根据S△ACD=3,即AC•DE=6,得到S△OAB=
AB•OB=
×(
×2)AC•DE=8,从而得到S△ODF=
S△OAB=2,进而求得反比例函数的解析式.
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 4 |
解答: 解:过D作DE⊥AB于E,作DF⊥OB于F,
解:过D作DE⊥AB于E,作DF⊥OB于F,
∵D为OA中点,
∴DE、DF是△OAB的中位线,
∴OB=2DE,
又∵AC=3BC,
∴AB=
AC,
又∵S△ACD=3,即AC•DE=6,
∴S△OAB=
AB•OB=
×(
×2)AC•DE=8,
∴S△ODF=
S△OAB=2,
∴k=-4.
故选D.
 解:过D作DE⊥AB于E,作DF⊥OB于F,
解:过D作DE⊥AB于E,作DF⊥OB于F,∵D为OA中点,
∴DE、DF是△OAB的中位线,
∴OB=2DE,
又∵AC=3BC,
∴AB=
| 4 |
| 3 |
又∵S△ACD=3,即AC•DE=6,
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
∴S△ODF=
| 1 |
| 4 |
∴k=-4.
故选D.
点评:本题考查了反比例函数的比例系数的几何意义,解题的关键是正确的求得三角形DOF的面积.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如果
a3xby与-a2ybx+1是同类项,则x+y的值为( )
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
 如图所示,下列能推出AD∥BC的条件是( )
如图所示,下列能推出AD∥BC的条件是( )| A、∠EAD=∠D |
| B、∠B=∠D |
| C、∠B+∠C=180° |
| D、∠EAD=∠B |
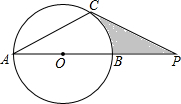 如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为( )
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为( )| A、8-2π | B、8-π |
| C、16-2π | D、16-π |
下列所给图形是中心对称图形但不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知⊙O及⊙O外一条直线l,作直线m∥直线l且与⊙O相切.(保留作图痕迹)
如图,已知⊙O及⊙O外一条直线l,作直线m∥直线l且与⊙O相切.(保留作图痕迹) 如图,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,函数y=
如图,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,函数y=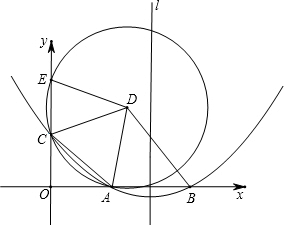 如图,抛物线y=
如图,抛物线y=