题目内容
 如图,抛物线y=
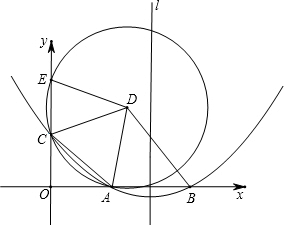
如图,抛物线y=
| ||
| 18 |
13
| ||
| 18 |
| 3 |
(1)求点A和点B的坐标;
(2)求△CDE的面积;
(3)点P为抛物线对称轴l上一点,点Q为抛物线上一点.若以P、Q、D、B为顶点的四边形为平行四边形,请直接写出点Q的横坐标.
考点:二次函数综合题
专题:
分析:(1)设y=0,则函数变为一元二次方程,解方程即可求出点A和点B的坐标;
(2)连结AE,作DF⊥CE于点F.则CF=
CE.在Rt△AOC中,利用勾股定理求出AC的长,进而得到AE,OE,CF的长,再根据三角形的面积公式计算即可;
(3)分两种情况考虑,Q在第一象限,以及第四象限,利用平行四边形的性质及坐标与图形性质求出Q坐标即可.
(2)连结AE,作DF⊥CE于点F.则CF=
| 1 |
| 2 |
(3)分两种情况考虑,Q在第一象限,以及第四象限,利用平行四边形的性质及坐标与图形性质求出Q坐标即可.
解答:解:(1)当y=0时,0=
x2-
x+2
,
整理得,x2-13x+36=0,
解得x1=4,x2=9,
∴A(4,0)、B(9,0);

(2)连结AE,作DF⊥CE于点F.则CF=
CE.
当x=0时,y=2
,
∴C(0,2
),
∴OC=2
.
∵OA=4,
在Rt△AOC中,AC=
=
=2
.
∵△ACD为等边三角形,
∴∠CDA=60°,
∴∠AEC=
∠CDA=30°.
∴AE=2OA=8.
在Rt△AOE中,OE=
=
=4
,
∴CE=OE-OC=2
.
∴CF=
CE=
.
在Rt△CDF中,DF=
=
=5.
∴S△CDE=
CE×DF=
×2
×5=5
.
(3)存在,
分两种情况考虑:
当Q在第一象限时,若四边形PQDB为平行四边形,
∵抛物线对称轴为直线x=6.5,
∴Q横坐标为10.5或2.5,
当Q在第四象限时Q的横坐标为7.5,
∴点Q的横坐标为10.5、7.5或2.5.
| ||
| 18 |
13
| ||
| 18 |
| 3 |
整理得,x2-13x+36=0,
解得x1=4,x2=9,
∴A(4,0)、B(9,0);

(2)连结AE,作DF⊥CE于点F.则CF=
| 1 |
| 2 |
当x=0时,y=2
| 3 |
∴C(0,2
| 3 |
∴OC=2
| 3 |
∵OA=4,
在Rt△AOC中,AC=
| AO2+OC2 |
| 16+12 |
| 7 |
∵△ACD为等边三角形,
∴∠CDA=60°,
∴∠AEC=
| 1 |
| 2 |
∴AE=2OA=8.
在Rt△AOE中,OE=
| EA2-OA2 |
| 82-42 |
| 3 |
∴CE=OE-OC=2
| 3 |
∴CF=
| 1 |
| 2 |
| 3 |
在Rt△CDF中,DF=
| CD2-CF2 |
| 28-3 |
∴S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(3)存在,
分两种情况考虑:
当Q在第一象限时,若四边形PQDB为平行四边形,
∵抛物线对称轴为直线x=6.5,
∴Q横坐标为10.5或2.5,
当Q在第四象限时Q的横坐标为7.5,
∴点Q的横坐标为10.5、7.5或2.5.
点评:此题属于二次函数综合题,涉及的知识有:抛物线和坐标轴的交点问题,平行四边形的性质,勾股定理的运用,三角形面积公式的运用,等边三角形的性质,利用了数形结合及分类讨论的思想,分类讨论时注意考虑问题要全面.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
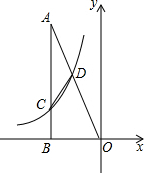 如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )
如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
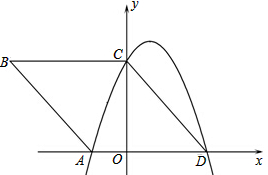 如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数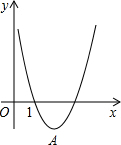 已知抛物线y=2x2-8x+6的顶点为A,如图.
已知抛物线y=2x2-8x+6的顶点为A,如图.