题目内容
18．
如图，在平行四边形ABCD中，AE=CF，AG⊥DE，CH⊥BF，求证：四边形EHFG是矩形．
分析 先证明四边形AECF、四边形BEDF是平行四边形，得出AF∥EC，DE∥FB，证出四边形EHFG是平行四边形，再由∠EGF=90°，即可得出四边形EHFG是矩形．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=DC，AB∥DC，
∵AE=CF，
∴BE=DF，
∴四边形AECF、四边形BEDF是平行四边形，
∴AF∥EC，DE∥FB，
∴四边形EHFG是平行四边形，
又∵AG⊥DE，
∴∠EGF=90°，
∴四边形EHFG是矩形．
点评 本题考查了平行四边形的性质与判定、矩形的判定；熟练掌握平行四边形的性质，并能进行推理论证是解决问题的关键．
练习册系列答案
相关题目
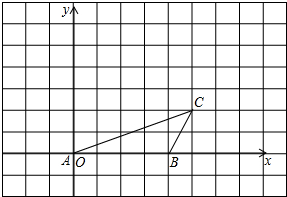
如图，在钝角△ABC中，BC=9，AB=17，AC=10，AD⊥BC于D，求AD的长．
如图，在△ABC中，AC=BC=2，∠ACB=90°，D是BC边上的中点，E是AB边上一动点，当EC+ED取最小值时，求△ECB的面积．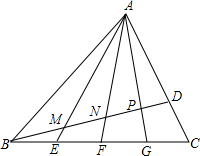
如图，已知△ABC中，D为AC边上一点，CD=$\frac{1}{3}$AC，点E、F、G四等分边BC，连接AE、AF、AG分别与BD交于点M、N、P，则BM：BD=$\frac{1}{3}$．
过正方体中有公共顶点的三条棱的中点，切去一个三棱锥，形成如图的几何体，其展开图正确的是（ ）
