题目内容
 如图,在△ABC中,∠A=68°,∠ABC=60°,CD平分∠ACB,BE为AC 边上的高,求∠BOC和∠ABE的度数.
如图,在△ABC中,∠A=68°,∠ABC=60°,CD平分∠ACB,BE为AC 边上的高,求∠BOC和∠ABE的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据三角形内角和定理求出∠ACB的度数,再由CD平分∠ACB得出∠ACD的度数.根据BE为AC 边上的高可知∠AEB=∠CEB=90°,由三角形外角的性质可知∠BOC=∠CEB+∠ACD,△ABE中根据三角形内角和定理即可得出结论.
解答:证明:∵∠A=68°,∠ABC=60°,
∴∠ACB=180°-∠A-∠ABC=52°.
∵CD平分∠ACB,
∴∠ACD=
∠ACB=26°.
∵BE为AC 边上的高,
∴∠AEB=∠CEB=90°,
∴∠BOC=∠CEB+∠ACD=90°+26°=116°.
∵∠A+∠AEB+∠ABE=180°,
∴∠ABE=180°-∠A-∠AEB=22°.
∴∠ACB=180°-∠A-∠ABC=52°.
∵CD平分∠ACB,
∴∠ACD=
| 1 |
| 2 |
∵BE为AC 边上的高,
∴∠AEB=∠CEB=90°,
∴∠BOC=∠CEB+∠ACD=90°+26°=116°.
∵∠A+∠AEB+∠ABE=180°,
∴∠ABE=180°-∠A-∠AEB=22°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
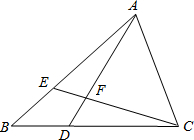 如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.
如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.