题目内容
若sinA=
,则cosA= .
| 2 |
| 5 |
考点:同角三角函数的关系
专题:
分析:根据同一锐角的正弦与余弦的平方和是1,即可求解.
解答:解:∵sin2A+cos2A=1,即(
)2+cos2A=1,
∴cos2A=
,
∴cosA=
或-
(舍去),
∴cosA=
.
故答案为:
.
| 2 |
| 5 |
∴cos2A=
| 21 |
| 25 |
∴cosA=
| ||
| 5 |
| ||
| 5 |
∴cosA=
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:此题主要考查了同角的三角函数,关键是掌握同一锐角的正弦与余弦之间的关系:对任一锐角α,都有sin2α+cos2α=1.

练习册系列答案
相关题目
 如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则
如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则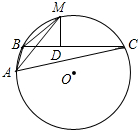 如图,
如图,
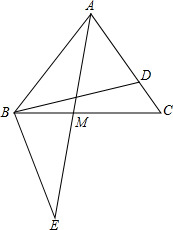 如图,在等边△ABC中,∠BDC+∠CBE=180°,BD=BE,AD:DC=3:1,求BM:CM.
如图,在等边△ABC中,∠BDC+∠CBE=180°,BD=BE,AD:DC=3:1,求BM:CM.