题目内容
1.计算:($\sqrt{18}$-$\sqrt{12}$)÷$\sqrt{6}$+2$\sqrt{\frac{1}{2}}$=$\sqrt{3}$.(结果保留根号)分析 先根据二次根式的除法运算,然后化简后合并即可.
解答 解:原式=$\sqrt{18÷6}$-$\sqrt{12÷6}$+$\sqrt{2}$
=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{2}$
=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.计算($\frac{3}{2}$)-2的结果是( )
| A. | $\frac{4}{9}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |
16.下列计算正确的是( )
| A. | (a4)2=a6 | B. | a+2a=3a2 | C. | a7÷a2=a5 | D. | a(a2+a+1)=a3+a2 |
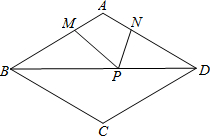 如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.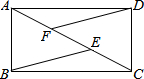 如图所示,E,F是矩形ABCD对角线AC上的两点,试添加一个条件:AF=CE,使得BE∥DF.
如图所示,E,F是矩形ABCD对角线AC上的两点,试添加一个条件:AF=CE,使得BE∥DF.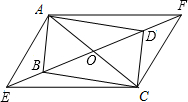 如图,?ABCD的对角线相交于点O,E、F在直线BD上,且BE=DF.
如图,?ABCD的对角线相交于点O,E、F在直线BD上,且BE=DF. 已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.