题目内容
10.用适当方法解下列二元一次方程组:(1)$\left\{\begin{array}{l}{3x+4y=19}\\{x-y=4}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-2y=5}\\{2x+3y=-1}\end{array}\right.$.
分析 (1)方程组整理后,利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=19①}\\{x-y=4②}\end{array}\right.$,
由②得:x=y+4③,
把③代入①得:3y+12+4y=19,
解得:y=1,
把y=1代入③得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-2y=5①}\\{2x+3y=-1②}\end{array}\right.$,
①×3+②×2得:13x=13,
解得:x=1,
把x=1代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
7.若实数x,y满足$\frac{1}{2}$y-xy+x2+2=0,则实数y满足的条件是( )
| A. | y≤-2 | B. | y≥4 | C. | y2-2y-8≥0 | D. | 一切实数 |
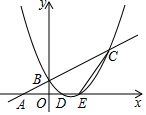 已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)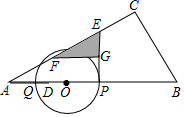 如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.
如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.