题目内容
解方程:4x2-10x+
=17.
| 2x2-5x+2 |
考点:无理方程
专题:计算题
分析:利用换元法解方程:设
=t,原方程转化为2t2+t-21=0,解此一元二次方程得到t1=3,t2=-
,再分别解
=3和
=-
,然后把解得的结果进行检验即可得到原方程的解.
| 2x2-5x+2 |
| 7 |
| 2 |
| 2x2-5x+2 |
| 2x2-5x+2 |
| 7 |
| 2 |
解答:解:方程变形为2(2x2-5x+2)-
-21=0
设
=t,
则原方程转化为2t2+t-21=0,
(t-3)(2t+7)=0,
解得t1=3,t2=-
,
当t=3时,
=3,则2x2-5x+2=9,
整理得2x2-5x-7=0,解得x1=
,x2=-1;
当t=-
时,
=-
,则方程无解,
经检验原方程的解为x1=
,x2=-1.
| 2x2-5x+2 |
设
| 2x2-5x+2 |
则原方程转化为2t2+t-21=0,
(t-3)(2t+7)=0,
解得t1=3,t2=-
| 7 |
| 2 |
当t=3时,
| 2x2-5x+2 |
整理得2x2-5x-7=0,解得x1=
| 7 |
| 2 |
当t=-
| 7 |
| 2 |
| 2x2-5x+2 |
| 7 |
| 2 |
经检验原方程的解为x1=
| 7 |
| 2 |
点评:本题考查了无理方程:方程中含有根式,且开方数是含有未知数的代数式,这样的方程叫做无理方程.解无理方程的基本思想是把无理方程转化为有理方程来解,在变形时要注意根据方程的结构特征选择解题方法.解无理方程,往往会产生增根,应注意验根.

练习册系列答案
相关题目
 如图,∠BDA=∠CEA,AE=AD.求证:AB=AC.
如图,∠BDA=∠CEA,AE=AD.求证:AB=AC.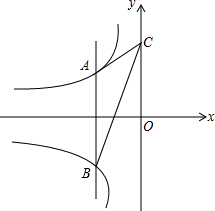 如图,动点A在双曲线y=-
如图,动点A在双曲线y=-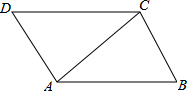 (1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA.
(1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA.