题目内容
10.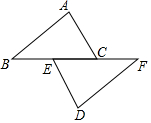 如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE.
如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE.
分析 在△ABC和△DFE中,根据AB=DF、AC=DE、BC=FE,利用全等三角形的判定定理SSS即可证出△ABC≌△DFE,进而得出∠ACB=∠DEF,再以及“内错角相等,两直线平行”即可证出结论.
解答 证明:在△ABC和△DFE中,$\left\{\begin{array}{l}{AB=DE}\\{BC=FE}\\{AC=DE}\end{array}\right.$,
∴△ABC≌△DFE(SSS),
∴∠ACB=∠DEF,
∴AC∥DE.
点评 本题考查了全等三角形的判定与性质以及平行线的判定,通过证全等三角形找出∠ACB=∠DEF是解题的关键.

练习册系列答案
相关题目
18.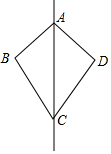 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
5.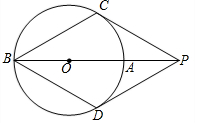 如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;
(2)四边形PCBD是菱形;
(3)PO=AB;
(4)∠PDB=120°.
其中,正确的个数是( )
 如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:(1)PD与⊙O相切;
(2)四边形PCBD是菱形;
(3)PO=AB;
(4)∠PDB=120°.
其中,正确的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.若点A(-4,y1),B(-1,y2),C(1,y3)在抛物线y=-$\frac{1}{2}$(x+2)2-1上,则( )
| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
20.下列方程为一元二次方程的是( )
| A. | 3x-2=0 | B. | x2-2x-3 | C. | x2-4x-1=0 | D. | xy+1=0 |
 如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.
如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.