题目内容
20. 如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.
如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.
分析 根据等边对等角可得∠B=∠C=30°,再根据线段垂直平分线的性质可得∠BAF=∠B=30°,进而可得∠FAC=90°,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得答案.
解答  解:连接AF,
解:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴AF=BF,
∴∠BAF=∠B=30°,
∴∠FAC=90°,
∵BF=5cm,
∴AF=5cm,
∴FC=10cm.
点评 此题主要考查了线段垂直平分线的性质,以及含30度角的直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半,垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
8.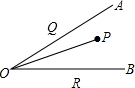 如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )
如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )
 如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )
如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
15.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下列代数式运算正确的是( )
| A. | 2a+3b=5ab | B. | a3+a2=a5 | C. | 5y2-3y2=2 | D. | x2y-2x2y=-x2y |
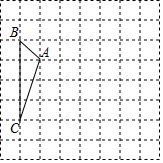 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.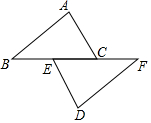 如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE.
如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE.