题目内容
15.若点A(-4,y1),B(-1,y2),C(1,y3)在抛物线y=-$\frac{1}{2}$(x+2)2-1上,则( )| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
分析 分别把-4、-1、1代入解析式进行计算,比较即可.
解答 解:y1=-$\frac{1}{2}$(-4+2)2-1=-3,
y2=-$\frac{1}{2}$(-1+2)2-1=-$\frac{3}{2}$,
y3=-$\frac{1}{2}$(1+2)2-1=-$\frac{11}{2}$,
则y3<y1<y2,
故选:D.
点评 本题考查的是二次函数图象上点的坐标特征,二次函数y=ax2+bx+c(a≠0)的图象上点的坐标满足其解析式.

练习册系列答案
相关题目
3.一元二次方程x2-6x+5=0配方后可变形为( )
| A. | (x-3)2=14 | B. | (x-3)2=4 | C. | (x+3)2=14 | D. | (x+3)2=4 |
20.若分式$\frac{x-2}{x+3}$有意义,则x的取值范围是( )
| A. | x≠2 | B. | x=-2 | C. | x=-3 | D. | x≠-3 |
4.如图图形中,轴对称图形的个数为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,⊙O与⊙O上一点P,用直尺和圆规过点P作⊙O切线(不写作法,保留作图痕迹),并写出作图依据.
如图,⊙O与⊙O上一点P,用直尺和圆规过点P作⊙O切线(不写作法,保留作图痕迹),并写出作图依据.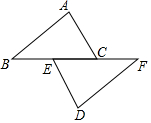 如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE.
如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,BC=FE.求证:AC∥DE. 斐波那契(约1170-1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]表示.
斐波那契(约1170-1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]表示.