��Ŀ����
4����֪����x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0��ʵ������kΪ����������1����k��ֵ��
��2�����˷��������������������ʱ��������x�Ķ��κ���y=x2+2x+$\frac{k-1}{2}$��ͼ������ƽ��9����λ����ƽ�ƺ��ͼ��ı���ʽ��
��3���ڣ�2���������£�ƽ�ƺ�Ķ��κ�����ͼ����x�ύ�ڵ�A��B����A�ڵ�B��ࣩ��ֱ��y=kx+b��k��0������B�����������ߵ���һ������ΪC��ֱ��BC�Ϸ������������߶�BC����µ�ͼ������ͼ�����Сֵ����-5ʱ����k��ȡֵ��Χ��
���� ��1�����ݷ�����ʵ�����ɵá���0�����k��ȡֵ��Χ��Ȼ�����kΪ�������ó�k��ֵ��
��2�����ݷ�������������������������жϣ��ó�k=3��Ȼ��ó���������ʽ��������ƽ�Ƶ��������ƽ�ƺ��ͼ��ı���ʽ��
��3����y=0���ó�A��B�����꣬����ͼ��Ȼ������º�������Сֵ����-5�����C�����꣬Ȼ�����B��C�����������ʱk��ֵ�����ɵó�k��ȡֵ��Χ��
��� �⣺��1���߹���x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0��ʵ������
���=b2-4ac=4-4��$\frac{k-1}{2}$��0��
��k-1��2��
��k��3��
��k��������
��k��ֵ��1��2��3��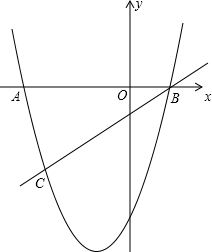
��2���߷����������������������
��k=1ʱ��x2+2x=0���������⣬��ȥ��
��k=2ʱ��x2+2x+$\frac{1}{2}$=0��
���̵ĸ������������������⣬��ȥ��
��k=3ʱ��x2+2x+1=0��
��ã�x1=x2=-1���������⣬
��k=3��
��y=x2+2x+1��
��ƽ�ƺ��ͼ��ı���ʽy=x2+2x+1-9=x2+2x-8��
��3����y=0��x2+2x-8=0��
��x1=-4��x2=2��
����x�ύ�ڵ�A��B����A�ڵ�B��ࣩ��
��A��-4��0����B��2��0����
��ֱ��l��y=kx+b��k��0��������B��
�ຯ����ͼ����ͼ��ʾ������C�������߶Գ������ʱ���º�������Сֵ�п��ܴ���-5��
��y=-5����x2+2x-8=-5��
��ã�x1=-3��x2=1�����������⣬��ȥ����
�������߾����㣨-3��-5����
��ֱ��y=kx+b��k��0�������㣨-3��-5������2��0��ʱ��
�����k=1��
��ͼ���֪����0��k��1ʱ�º�������Сֵ����-5��
���� ���⿼���˶��κ������ۺ�Ӧ�ã��漰�˸����б�ʽ��ͼ���ƽ�ƣ����κ����Ľ��������֪ʶ�������Ĺؼ��Ǹ���ͼ���Լ���������ʽ���з�����⣬�Ѷ�һ�㣮

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�| A�� | 3cm��5cm��8cm | B�� | 8cm��8cm��18cm | C�� | 4cm��4cm��4cm | D�� | 3cm��40cm��8cm |
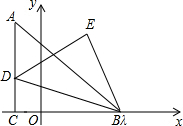 ��֪Rt��ABC�У���ACB=90�㣬AC=BC���ҵ�B��a+1��0����C��b��0������ƽ��ֱ������ϵ��x���ϣ���ͼ��ʾ��������a2+b2-10a+4b+29=0����DΪ����AC��һ������������Ϊm����BDΪб�ߣ���˳ʱ��˳������BDE��ʹ��DEB=90�㣬EB=ED��
��֪Rt��ABC�У���ACB=90�㣬AC=BC���ҵ�B��a+1��0����C��b��0������ƽ��ֱ������ϵ��x���ϣ���ͼ��ʾ��������a2+b2-10a+4b+29=0����DΪ����AC��һ������������Ϊm����BDΪб�ߣ���˳ʱ��˳������BDE��ʹ��DEB=90�㣬EB=ED��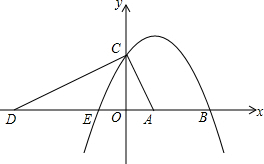 ��ͼ��������y=ax2+bx+c��a��0����x���ཻ������E��B��E��B����ࣩ����y���ཻ�ڵ�C��0��2������D������Ϊ��-4��0������AB=AE=2����ACD=90�㣮
��ͼ��������y=ax2+bx+c��a��0����x���ཻ������E��B��E��B����ࣩ����y���ཻ�ڵ�C��0��2������D������Ϊ��-4��0������AB=AE=2����ACD=90�㣮