题目内容
17.若关于x的分式方程$\frac{k}{k+2}$+$\frac{1}{{x}^{2}-4}$=0有实数解,则k的取值范围是k≥$\frac{2}{3}$或k<0(k≠-2).分析 分式方程去分母转化为整式方程,由分式方程有解确定出k的范围即可.
解答 解:去分母得:kx2-4k+k+2=0,即x2=$\frac{3k-2}{k}$,
由分式方程有实数解,得到$\frac{3k-2}{k}$≥0,且$\frac{3k-2}{k}$≠4,即$\left\{\begin{array}{l}{3k-2≥0}\\{k>0}\end{array}\right.$或$\left\{\begin{array}{l}{3k-2≤0}\\{k<0}\end{array}\right.$(k≠-2),
解得:k≥$\frac{2}{3}$或k<0(k≠-2),
故答案为:k≥$\frac{2}{3}$或k<0(k≠-2)
点评 此题考查了分式方程的解,始终注意分式方程分母不为0这个条件.

练习册系列答案
相关题目
8.直线y=x与直线y=2x+1的交点坐标是( )
| A. | (0,1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
5.两个一次函数y=2x-$\frac{1}{2}$与y=-x+$\frac{2}{3}$的图象交点坐标为( )
| A. | ($\frac{7}{18},\frac{5}{18}$) | B. | ($\frac{1}{2},\frac{2}{3}$) | C. | ($\frac{2}{3},\frac{1}{2}$) | D. | ($\frac{7}{6},\frac{5}{6}$) |
12.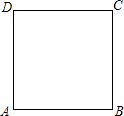 如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
 如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )| A. | $\sqrt{17}$ | B. | 3 | C. | 5 | D. | 2$\sqrt{5}$ |
9.数据x1,x2,…,xn的极差为0,则这组数据的方差为( )
| A. | 1 | B. | 0 | C. | n2 | D. | 不能确定 |
 一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①k<0;②两直线交于点(3,1);③当x<3时,y1<y2.其中正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①k<0;②两直线交于点(3,1);③当x<3时,y1<y2.其中正确的个数是( ) 如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.
如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.