题目内容
11．（1）解方程：（x-4）2=x-4；（2）解不等式组：$\left\{\begin{array}{l}{3（x+1）＜5x}\\{\frac{1}{3}x-1≤7-\frac{5}{3}x}\end{array}\right.$．
分析 （1）因式分解法求解可得；
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：（1）∵（x-4）2-（x-4）=0，
∴（x-4）（x-5）=0，
则x-4=0或x-5=0，
解得：x=4或x=5；
（2）解不等式3（x+1）＜5x，得：x＞$\frac{3}{2}$，
解不等式$\frac{1}{3}$x-1≤7-$\frac{5}{3}$x，得：x≤4，
∴不等式组的解集为$\frac{3}{2}$＜x≤4．
点评 本题主要考查解一元二次方程和一元一次不等式的能力，熟练掌握解一元一次不等式的基本步骤和解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
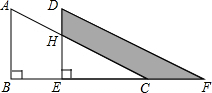如图，将Rt△ABC沿射线BC方向平移得到△DEF，已知AB=16cm，BE=10cm，DH=6cm，则图中阴影部分的面积为130cm2．
如图，P为直线l外一点，A、B、C在l上，且PB⊥l，下列说法中，正确的个数是（ ）
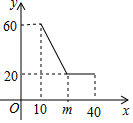经市场调查，某公司生产的大白公仔的每天的销售量y（件）与销售价格x（元/件）之间的函数关系如图所示．
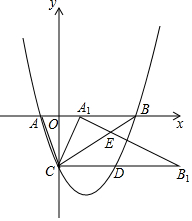如图，已知抛物线与y轴交于点C（0，-3），与x轴交于点A（-1，0）B（4，0），将△ABC绕点C顺时针旋转α得△A1B1C（点A，B的对应点分别为点A1，B1），CB1交抛物线于点D，射线A1B1与射线BC交于点E．
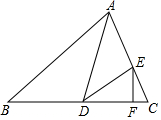如图，在△ABC中，∠B=50°，AD平分∠CAB，交BC于D，E为AC边上一点，连接DE，∠EAD=∠EDA，EF⊥BC于点F．求∠FED的度数．