题目内容
19.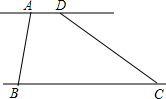 在一次数学活动课上.老师带领同学们去侧量一条两岸平行的河的宽度,在河岸的一边有两棵相距30m的大树B.C,某同学在河岸另一边点A处现测树B,侧得∠ABC=70°,他又沿河岸前行10m到达D处,测得∠DCB=37°,请计算河的宽度.(结果精确到0.01m)
在一次数学活动课上.老师带领同学们去侧量一条两岸平行的河的宽度,在河岸的一边有两棵相距30m的大树B.C,某同学在河岸另一边点A处现测树B,侧得∠ABC=70°,他又沿河岸前行10m到达D处,测得∠DCB=37°,请计算河的宽度.(结果精确到0.01m)参考数据:sin70°≈$\frac{15}{16}$,cos70°≈$\frac{1}{10}$,tan70°≈$\frac{11}{4}$,sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
分析 作AE⊥BC于E,DF⊥BC于F,设河的宽度为xm,根据正切的概念用x表示出BE、FC的长,根据题意列出方程,解方程即可.
解答 解: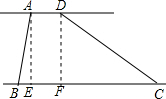 作AE⊥BC于E,DF⊥BC于F,
作AE⊥BC于E,DF⊥BC于F,
则EF=AD=10m,
设河的宽度为xm,
∵tanB=$\frac{AE}{BE}$,
∴BE=$\frac{4}{11}$x,
∵tanC=$\frac{DF}{FC}$,
∴FC=$\frac{4}{3}$x,
由题意得,$\frac{4}{11}$x+10+$\frac{4}{3}$x=30,
解得x=$\frac{165}{14}$≈11.79.
答:河的宽度约为11.79m.
点评 本题考查的是解直角三角形的应用,正切作出辅助线、构造出直角三角形、灵活运用锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
9.多项式2x3-x2y2+y3+25的次数和项数分别是( )
| A. | 5次4项 | B. | 3次4项 | C. | 4次4项 | D. | 无法确定 |
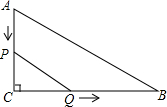 在△ABC中,∠C=90°,AC=11,点P从点A沿AC向C点以每秒1cm的速度移动,同时,点Q从点C沿CB向B点以每秒2cm的速度移动.
在△ABC中,∠C=90°,AC=11,点P从点A沿AC向C点以每秒1cm的速度移动,同时,点Q从点C沿CB向B点以每秒2cm的速度移动.