题目内容
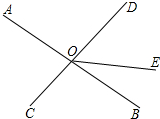 如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;
(2)画射线OF⊥OE,求∠DOF的度数.
考点:对顶角、邻补角,角的计算
专题:
分析:(1)根据对顶角相等可得∠BOD=∠AOC,然后根据比例求解即可;
(2)先求出∠DOE,再分OF在∠AOD的内部时,∠DOF=∠EOF-∠DOE,OF在∠BOC的内部时,∠DOF=∠DOE+∠EOF进行计算即可得解.
(2)先求出∠DOE,再分OF在∠AOD的内部时,∠DOF=∠EOF-∠DOE,OF在∠BOC的内部时,∠DOF=∠DOE+∠EOF进行计算即可得解.
解答:解: (1)∵∠AOC=75°,
(1)∵∠AOC=75°,
∴∠BOD=∠AOC=75°,
∵∠BOE:∠EOD=2:3,
∴∠BOE=75°×
=30°;
(2)∠DOE=∠BOD-∠BOE=75°-30°=45°,
∵OF⊥OE,
∴∠EOF=90°,
OF在∠AOD的内部时,∠DOF=∠EOF-∠DOE,
=90°-45°,
=45°,
OF在∠BOC的内部时,∠DOF=∠DOE+∠EOF,
=90°+45°,
=135°,
综上所述∠DOF=45°或135°.
 (1)∵∠AOC=75°,
(1)∵∠AOC=75°,∴∠BOD=∠AOC=75°,
∵∠BOE:∠EOD=2:3,
∴∠BOE=75°×
| 2 |
| 2+3 |
(2)∠DOE=∠BOD-∠BOE=75°-30°=45°,
∵OF⊥OE,
∴∠EOF=90°,
OF在∠AOD的内部时,∠DOF=∠EOF-∠DOE,
=90°-45°,
=45°,
OF在∠BOC的内部时,∠DOF=∠DOE+∠EOF,
=90°+45°,
=135°,
综上所述∠DOF=45°或135°.
点评:本题考查了对顶角相等的性质,角的计算,熟记概念并准确识图是解题的关键.

练习册系列答案
相关题目
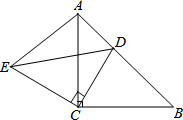 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点, 如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°.1s后,火箭到达B点,此时测得BC的距离是6.27km,仰角为45.32°,解答下列问题:
如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°.1s后,火箭到达B点,此时测得BC的距离是6.27km,仰角为45.32°,解答下列问题: 如图,CE是△ABC的外角∠ACD的角平分线,且CE交BA的延长线于点E,求证:∠BAC=∠B+2∠E.
如图,CE是△ABC的外角∠ACD的角平分线,且CE交BA的延长线于点E,求证:∠BAC=∠B+2∠E.