题目内容
已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列三个结论:①a<0;②a+b+c>0;③-
>0,则正确的结论有( )
| b |
| 2a |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线经过点(-1,0),且顶点在第一象限,判断抛物线开口向下,且对称轴在y轴的右侧,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答: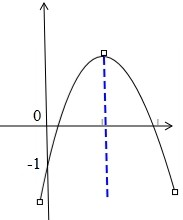 解:如图:
解:如图:
∵抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限,
∴抛物线开口向下,且对称轴在y轴的右侧,
即a<0,x=-
>0
∴b>0,故①③正确;
由题意不能确定当x=1时,y与0的大小,故②错误,故有2个正确.
故选:C.
 解:如图:
解:如图:∵抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限,
∴抛物线开口向下,且对称轴在y轴的右侧,
即a<0,x=-
| b |
| 2a |
∴b>0,故①③正确;
由题意不能确定当x=1时,y与0的大小,故②错误,故有2个正确.
故选:C.
点评:本题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
 如图,阴影部分是一个正方形,该正方形的面积为( )cm2.
如图,阴影部分是一个正方形,该正方形的面积为( )cm2.| A、25 | B、5 | C、313 | D、20 |
使等式
=
成立的实数m的取值范围是( )
|
| ||
|
A、m>3或m<
| ||
| B、0<m<3 | ||
C、m≥
| ||
| D、m>3 |
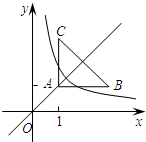 如图,直角三角形ABC位于第一象限,AB=3,AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=
如图,直角三角形ABC位于第一象限,AB=3,AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=| k |
| x |
| A、1≤k≤5 | ||
B、1≤k≤
| ||
C、1≤k≤
| ||
D、1≤k≤
|
 如图,山顶建有一座铁塔,塔高CD=30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB.
如图,山顶建有一座铁塔,塔高CD=30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB.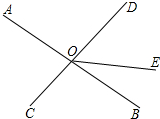 如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.