题目内容
13. 如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=$\frac{2}{3}$,E是$\widehat{AB}$的中点,求EG•ED的值.
分析 (1)直接利用圆周角定理得出AD⊥BC,再利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;
(2)利用圆内接四边形的性质得出∠AFD=180°-∠E,进而得出∠BDF=∠C+∠CFD,即可得出答案;
(3)根据cosB=$\frac{2}{3}$,得出AB的长,即可求出AE的长,再判断△AEG∽△DEA,求出EG•ED的值.
解答 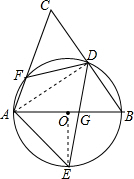 (1)证明:连接AD,
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°-∠E,
又∵∠CFD=180°-∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=$\frac{2}{3}$,BD=4,
∴AB=6,
∵E是$\widehat{AB}$的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3$\sqrt{2}$,
∵E是$\widehat{AB}$的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴$\frac{AE}{EG}$=$\frac{DE}{AE}$,
即EG•ED=AE2=18.
点评 此题主要考查了圆的综合题、圆周角定理以及相似三角形的判定与性质以及圆内接四边形的性质等知识,根据题意得出AE,AB的长是解题关键.

练习册系列答案
相关题目
3.从0,π,$\frac{1}{3}$,$\frac{{\sqrt{2}}}{2}$这四个数中随机取出一个数,取出的数是无理数的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
4.若x2-3y-5=0,则6y-2x2-6的值为( )
| A. | 4 | B. | -4 | C. | 16 | D. | -16 |
2.在郴州市中小学“创园林城市,创卫生城市,创文明城市”演讲比赛中,5位评委给靓靓同学的评分如下:9.0,9.2,9.2,9.1,9.5,则这5个数据的平均数和众数分别是( )
| A. | 9.1,9.2 | B. | 9.2,9.2 | C. | 9.2,9.3 | D. | 9.3,9.2 |
3. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )| A. | DE=$\frac{1}{2}$BC | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | △ADE∽△ABC | D. | S△ADE:S△ABC=1:2 |
 下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )



 如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法) 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件AD∥BC(写一个即可),使四边形ABCD是平行四边形.
如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件AD∥BC(写一个即可),使四边形ABCD是平行四边形.