题目内容
7. 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,求BF.
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,求BF.
分析 由矩形ABCD,得到两组对边相等,四个角为直角,再由折叠的性质得到三角形ADE与三角形AEF全等,利用全等三角形的对应边相等得到AD=AF,DE=EF,由AB-EC求出DE的长,即为EF的长,在直角三角形ECF中,利用勾股定理求出FC的长,设BF=x,表示出AF,在直角三角形ABF中,利用勾股定理求出x的值,即可确定出BF的长.
解答 解:∵四边形ABCD为矩形,
∴AB=CD,AD=BC,∠B=∠C=∠D=90°,
由折叠的性质得:AD=AF,DE=EF,∠AFE=∠D=90°,
∵CE=3,AB=8,
∴EF=DE=DC-EC=AB-EC=8-3=5,
在Rt△ECF中,EF=5,EC=3,
根据勾股定理得:FC=4,
设BF=x,AD=BC=AF=BF+FC=x+4,
在Rt△ABF中,AF=x+4,BF=x,AB=8,
根据勾股定理得:x2+82=(x+4)2,
解得:x=6,
则BF=6.
点评 此题考查了翻折变换(折叠问题),勾股定理,利用了方程的思想,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
18.若分式$\frac{x+y}{2xy}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
15.计算(-a3)2的结果是( )
| A. | a6 | B. | -a6 | C. | a5 | D. | -a5 |
12.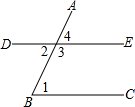 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
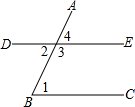 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠1和∠2是同位角 | B. | ∠1和∠4是内错角 | ||
| C. | ∠1和∠3是内错角 | D. | ∠1和∠3是同旁内角 |
16.下列说法中正确的是( )
| A. | 若式子$\sqrt{x-1}$有意义,则x>1 | |
| B. | 已知a,b,c,d都是正实数,且$\frac{a}{b}$<$\frac{c}{d}$,则$\frac{b}{a+b}$<$\frac{d}{c+d}$ | |
| C. | 解分式方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的结果是原方程无解. | |
| D. | 在反比例函数y=$\frac{k-2}{x}$中,若x>0时,y随x的增大而增大,则k的取值范围是k>2 |
17.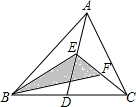 如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4,则S△BFF=( )
如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4,则S△BFF=( )
 如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4,则S△BFF=( )
如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4,则S△BFF=( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25 cm2 |
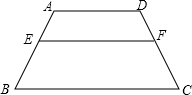 如图,已知:AD∥BC,∠AEF=∠B,求证:AD∥EF.
如图,已知:AD∥BC,∠AEF=∠B,求证:AD∥EF.