题目内容
19.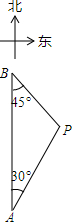 如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 过点P作PC⊥AB,C是垂足.AC与BC就都可以根据三角函数用PC表示出来.根据AB的长,得到一个关于PC的方程,解出PC的长.从而判断出这条高速公路会不会穿越森林保护区.
解答  解:过点P作PC⊥AB,C是垂足,则∠A=30°,∠B=45°,
解:过点P作PC⊥AB,C是垂足,则∠A=30°,∠B=45°,
AC=$\frac{PC}{tan30°}$=$\sqrt{3}$PC,BC=$\frac{PC}{tan45°}$=PC.
∵AC+BC=AB,
∴$\sqrt{3}$PC+PC=100,
∴PC=50($\sqrt{3}$-1)≈50×(1.732-1)=36.6>35.
答:森林保护区的中心与直线AB的距离大于保护区的半径,所以计划修筑的这条高速公路不会穿越保护区.
点评 本题主要考查解直角三角形的应用-方向角问题,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
10.下列各数中,是无理数的是( )
| A. | $\sqrt{9}$ | B. | $\frac{24}{7}$ | C. | $\frac{π}{2}$ | D. | $\root{3}{8}$ |
7.国家规定存款利息的纳税办法是:利息税=利息×20%,银行一年定期的利率为2.25%,屠呦呦获得诺贝尔医学奖,假设她把所有奖金存入银行一年,预计一年到期后,提取本金及利息时要交纳13500元利息税,则屠呦呦的奖金是( )元.
| A. | 3×105 | B. | 3×106 | C. | 3×107 | D. | 3×108 |
9.在比例尺是1:46000的城市交通游览图上,某条道路的图上距离长约8cm,则这条道路的实际长度约为( )
| A. | 368×103cm | B. | 36.8×104cm | C. | 3.68×105cm | D. | 3.68×106cm |
 如图,把一幅三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为$\sqrt{13}$.
如图,把一幅三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为$\sqrt{13}$.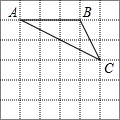 在如图所示的方格纸中,每个小正方形的边长都为1,点A、B、C均为格点(每个小正方形的顶点称为格点).
在如图所示的方格纸中,每个小正方形的边长都为1,点A、B、C均为格点(每个小正方形的顶点称为格点).