题目内容
9. 如图,把一幅三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为$\sqrt{13}$.
如图,把一幅三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为$\sqrt{13}$.
分析 首先由旋转的角度为15°,可知∠ACD1=45°.已知∠CAO=45°,即可得AO⊥CD1,然后可在Rt△AOC和Rt△AOD1中,通过解直角三角形求得AD1的长.
解答 解:由题意易知:∠CAB=45°,∠ACD=30°.
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=4,则AC=BC=2$\sqrt{2}$.
同理可得:AO=OC=2.
在Rt△AOD1中,OA=2,OD1=CD1-OC=3,
由勾股定理得:AD1=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 此题主要考查了旋转的性质以及解直角三角形的综合应用,能够发现AO⊥OC是解决此题的关键.

练习册系列答案
相关题目
19.某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参考数据如表:
(1)请分别写出汽车、火车运输总费用y1(元)、y2(元)与运输路程x(千米)之间的函数表达式;
(2)你认为用哪种运输方式好?
| 运输方式 | 速度/(千米/时) | 途中综合费用/(元/时) | 装卸费用/(元) |
| 汽车 | 60 | 270 | 200 |
| 火车 | 100 | 240 | 410 |
(2)你认为用哪种运输方式好?
17.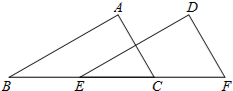 如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
 如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )| A. | BE=CF | B. | AC=DF | C. | AC∥DF | D. | ∠A=∠D |
14.某旅行社为吸引市民组团去某景区旅游,推出如下收费标准:
某单位组织员工去该风景区旅游,设有x人参加,应付旅游费y元.
(1)请写出y与x的函数关系式;
(2)若该单位现有36人,本次旅游至少去31人,则该单位最多应付旅游费多少元?
| 人数 | 不超过30人 | 超过30人但不超过40人 | 超过40人 |
| 人均旅游费 | 1000元 | 每增加1人,人均旅游费降低20元 | 800元 |
(1)请写出y与x的函数关系式;
(2)若该单位现有36人,本次旅游至少去31人,则该单位最多应付旅游费多少元?
 如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.
如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.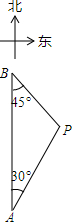 如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)