题目内容
17.如果最简二次根式$\root{b-a}{3b}$和$\sqrt{2b-a+2}$可以合并,那么a=0,b=2.分析 根据最简二次根式能够合并得出方程组,求出方程组的解即可.
解答 解:∵最简二次根式$\root{b-a}{3b}$和$\sqrt{2b-a+2}$可以合并,
∴$\left\{\begin{array}{l}{b-a=2}\\{3b=2b-a+2}\end{array}\right.$,
解得:a=0,b=2,
故答案为:0,2.
点评 本题考查了最简二次根式和同类二次根式、二元一次方程组等知识点,能得出关于a、b的方程组是解此题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.下列方程组中哪一个是二元一次方程组( )
| A. | $\left\{\begin{array}{l}{m-n=1}\\{m+n=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-z=0}\\{x+y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=1}\\{xy=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=1}\\{\frac{1}{x}-\frac{1}{y}=32}\end{array}\right.$ |
7.已知am=8,an=16,则am+n等于( )
| A. | 24 | B. | 32 | C. | 64 | D. | 128 |
 在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=$\left\{\begin{array}{l}{x-y(当x≥y时)}\\{y-x(当x<y时)}\end{array}\right.$,那么称点Q为点P的“关联点”.
在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=$\left\{\begin{array}{l}{x-y(当x≥y时)}\\{y-x(当x<y时)}\end{array}\right.$,那么称点Q为点P的“关联点”.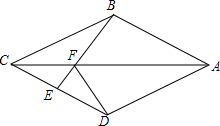 如图,在四边形ABCD中,AB=AD、CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD、CB=CD,E是CD上一点,BE交AC于F,连接DF.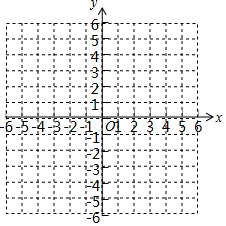 已知:A(0,1),B(2,0),C(4,3)
已知:A(0,1),B(2,0),C(4,3)