题目内容
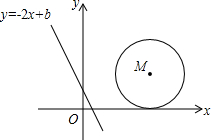 如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b=
如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b=考点:切线的判定,一次函数的性质
专题:计算题
分析:先求出直线y=-2x+b与坐标轴的交点A坐标为(0,b),B点坐标为(
,0),再计算出当直线y=-2x+b过点M时与y轴的交点D的坐标(0,8),如图,作MF⊥AB于F,AE⊥DC于E,根据切线的性质得MF=2,则AE=MF=2,再证明△OAB∽△EDA,利用相似比得到
=
,解得b=8-2
,利用直线平移的方法可得当b=8+2
时,直线y=-2x+b与⊙M相切.
| b |
| 2 |
| ||||
| 8-b |
| ||
| 2 |
| 5 |
| 5 |
解答:解: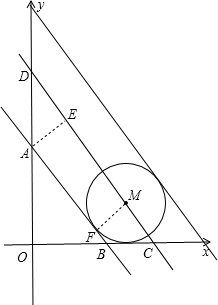 当x=0时,y=-2x+b=b,则A点坐标为(0,b);当y=0时,-2x+b=0,解得x=
当x=0时,y=-2x+b=b,则A点坐标为(0,b);当y=0时,-2x+b=0,解得x=
,则B(
,0),
所以AB=
=
a,
当直线y=-2x+b过点M时,把M(3,2)代入得-6+b=2,解得b=8,
则直线y=-2x+8与y轴的交点坐标为(0,8),
当AB与⊙M相切时,如图,作MF⊥AB于F,AE⊥DC于E,则AE=MF=2,
∵CD∥AB,
∴△OAB∽△EDA,
∴
=
,即
=
,解得b=8-2
,
同样可得当b=8+2
时,直线y=-2x+b与⊙M相切.
故答案为8±2
.
 当x=0时,y=-2x+b=b,则A点坐标为(0,b);当y=0时,-2x+b=0,解得x=
当x=0时,y=-2x+b=b,则A点坐标为(0,b);当y=0时,-2x+b=0,解得x=| b |
| 2 |
| b |
| 2 |
所以AB=
| OA2+OB2 |
| ||
| 2 |
当直线y=-2x+b过点M时,把M(3,2)代入得-6+b=2,解得b=8,
则直线y=-2x+8与y轴的交点坐标为(0,8),
当AB与⊙M相切时,如图,作MF⊥AB于F,AE⊥DC于E,则AE=MF=2,
∵CD∥AB,
∴△OAB∽△EDA,
∴
| AB |
| AD |
| OB |
| AE |
| ||||
| 8-b |
| ||
| 2 |
| 5 |
同样可得当b=8+2
| 5 |
故答案为8±2
| 5 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了一次函数性质.

练习册系列答案
相关题目
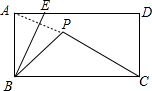 如图所示,长方形ABCD中,AB=4,BC=8,点E是折线段A-D-C上的一个动点,点P是点A关于BE的对称点,在点E运动的过程中,能使△PCB为等腰三角形的点E的位置共有( )个.
如图所示,长方形ABCD中,AB=4,BC=8,点E是折线段A-D-C上的一个动点,点P是点A关于BE的对称点,在点E运动的过程中,能使△PCB为等腰三角形的点E的位置共有( )个.| A、2个 | B、3个 | C、4个 | D、5个 |
已知△ABC的三个顶点都在⊙O上,AB=AC,⊙O的半径等于5cm,圆心O到BC的距离为3cm,则AB的长等于( )
A、2
| ||||
B、2
| ||||
C、4
| ||||
D、2
|
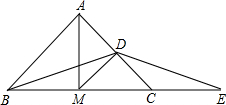 已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=
已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=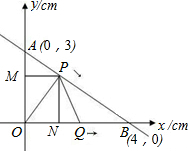 已知,Rt△ABC中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB边、OB边上的动点,它们同时分别从A、O向B匀速移动,速度都为1cm/s,设PQ移动时间为ts(0≤t≤4).
已知,Rt△ABC中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB边、OB边上的动点,它们同时分别从A、O向B匀速移动,速度都为1cm/s,设PQ移动时间为ts(0≤t≤4).