题目内容
已知x2-4x+1=0,求:
(1)x2+
;
(2)(x-
)2.
(1)x2+
| 1 |
| x2 |
(2)(x-
| 1 |
| x |
考点:完全平方公式
专题:计算题
分析:(1)已知等式变形求出x+
=4,两边平方即可求出原式的值;
(2)原式利用完全平方公式化简,将各自的值代入计算即可求出值.
| 1 |
| x |
(2)原式利用完全平方公式化简,将各自的值代入计算即可求出值.
解答:解:(1)已知等式x2-4x+1=0,变形得:x+
=4,
两边平方得:(x+
)2=x2+
+2=16,
则x2+
=14;
(2)(x-
)2=x2+
-2=14-2=12.
| 1 |
| x |
两边平方得:(x+
| 1 |
| x |
| 1 |
| x2 |
则x2+
| 1 |
| x2 |
(2)(x-
| 1 |
| x |
| 1 |
| x2 |
点评:此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
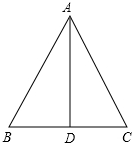 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.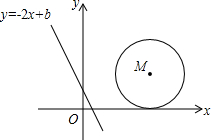 如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b=
如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b=