Question

17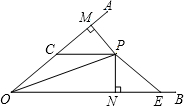．如图，OP平分∠AOB，∠AOB=40°，PM⊥OA于M，PN⊥OB于N，PC∥OB，交边OA于点C，E为边OB上的一点，且满足PC=PE．求∠EPN的度数？

Answer 1

分析 根据角平分线上的点到角的两边距离相等可得PM=PN，然后利用“HL”证明Rt△PMC和Rt△PNE全等，根据全等三角形对应角相等可得∠EPN=∠CPM，根据两直线平行，同位角相等可得∠PCM=∠AOB，再根据直角三角形两锐角互余列式计算即可得解．

解答 解：∵OP平分∠AOB，PM⊥OA，PN⊥OB，
∴PM=PN，
在Rt△PMC和Rt△PNE中，
$\left\{\begin{array}{l}{PC=PE}\\{PM=PN}\end{array}\right.$，
∴Rt△PMC≌Rt△PNE（HL），
∴∠EPN=∠CPM，
∵PC∥OB，
∴∠PCM=∠AOB=40°，
∵PM⊥AO，
∴∠CPM=90°-40°=50°，
∴∠EPN=50°．

点评 本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，平行线的性质，熟记性质并确定出全等三角形是解题的关键．