题目内容
1．
如图，△ABC中，DE∥BC，DE=2，AD=4，DB=6，则BC的长是（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 根据平行线分线段成比例得出$\frac{AD}{AB}$=$\frac{DE}{BC}$，再把相应的数据代入计算即可求出BC．
解答 解：∵DE∥BC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∵AB=AD+DB，
∴$\frac{AD}{AD+DB}$=$\frac{DE}{BC}$，
∵DE=2，AD=4，DB=6，
∴$\frac{4}{4+6}$=$\frac{2}{BC}$，
∴BC=5；
故选D．
点评 本题主要考查平行线分线段成比例的性质，掌握平行线分线段成比例中的对应线段是解题的关键．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
11．要使$\frac{\sqrt{x-4}}{x-5}$有意义，则x的取值范围是（ ）
| A． | x＞4 | B． | x≠5 | C． | x≥4且x≠5 | D． | x≠5 |
6．
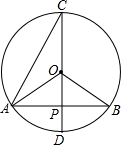如图，⊙O中，CD是直径，且CD⊥AB于P，则下列结论中不一定正确的是（ ）
如图，⊙O中，CD是直径，且CD⊥AB于P，则下列结论中不一定正确的是（ ）| A． | AP=PB | B． | $\widehat{AD}$=$\widehat{BD}$ | C． | ∠AOB=4∠ACD | D． | PO=PD |