题目内容
1．
如图，Rt△ABC中，∠C=90°，AB=10，AC=8，E是AC上一点，AE=5，ED⊥AB于D．（1）求证：△ACB∽△ADE；
（2）求AD的长度．
分析 （1）求出∠EDA=∠C=90°，根据相似三角形的判定得出相似即可；
（2）根据相似得出比例式，代入求出即可．
解答 （1）证明：∵DE⊥AB，∠C=90°，
∴∠EDA=∠C=90°，
∵∠A=∠A，
∴△ACB∽△ADE；
（2）解：∵△ACB∽△ADE，
∴$\frac{AE}{AB}$=$\frac{AD}{AC}$，
∴$\frac{5}{10}$=$\frac{AD}{8}$，
∴AD=4．
点评 本题考查了相似三角形的性质和判定的应用，能推出△ACB∽△ADE是解此题的关键．
练习册系列答案
相关题目
11．
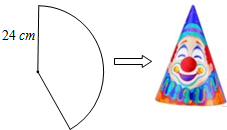小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的面积是（ ）
小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的面积是（ ）| A． | 120πcm2 | B． | 240πcm2 | C． | 260πcm2 | D． | 480πcm2 |
9．下列各点中关于原点对称的两个点是（ ）
| A． | （-5，0）和（0，5） | B． | （2，-1）和（1，-2） | C． | （5，0）和（0，-5） | D． | （-2，-1）和（2，1） |
6．关于x的一元二次方程（m-1）x2-x+m2-1=0的一个解是0，则m的值为（ ）
| A． | 0 | B． | ±1 | C． | 1 | D． | -1 |