题目内容
13.某公司经销一种绿茶,每千克成本为60元,市场调查发现,在一段时间内,销售量w(千克)随着销售单价x(元/千克)的变化而变化,具体关系式为:w=-2x+280,设这种绿茶在这段时间的销售利润为y(元).(1)求y和x的关系式;
(2)当销售单价为多少元时,该公司获取的销售利润最大?最大利润是多少?
分析 (1)根据销售利润=每千克利润×总销量,因为y=(x-60)w,w=-2x+280,进而求出即可.
(2)用配方法化简函数式求出y的最大值即可.
解答 解:(1)∵w=(x-60)•w=(x-60)•(-2x+280)=-2x2+400x-16800,
∴y与x的关系式为:y=-2x2+400x-16800.
(2)y=-2x2+400x-16800=-2(x-100)2+3200,
故当x=100时,y的值最大值是3200.
点评 此题主要考查了二次函数的实际应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
相关题目
8. 如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2),有下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2),有下列结论:
①a>0;
②b2-4ac>0;
③当x<1时,y随x的增大而减小;
④当0<x<1时,y>2.
其中正确的结论有( )
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2),有下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2),有下列结论:①a>0;
②b2-4ac>0;
③当x<1时,y随x的增大而减小;
④当0<x<1时,y>2.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.计算(-3)-(-5)=( )
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
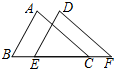 已知:如图,E、C是BF上两点,且AB∥DE,BE=FC,∠A=∠D.求证:AC=DF.
已知:如图,E、C是BF上两点,且AB∥DE,BE=FC,∠A=∠D.求证:AC=DF. 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D. 从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是圆柱.
从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是圆柱. 如图,tan∠ABC=$\frac{\sqrt{3}}{3}$.
如图,tan∠ABC=$\frac{\sqrt{3}}{3}$.