题目内容
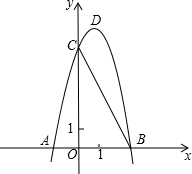 如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求
如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求(1)抛物线的解析式;
(2)若抛物线上有一点N,使得直线ON将△BOC的面积分成相等的两部分,求点N的坐标.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)根据已知求得B、C的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)先求得BC的中点坐标,然后求得经过中点和原点的直线,和抛物线的解析式联立方程,求得方程组的解即可求得N的坐标.
(2)先求得BC的中点坐标,然后求得经过中点和原点的直线,和抛物线的解析式联立方程,求得方程组的解即可求得N的坐标.
解答:解:(1)∵抛物线y=ax2+bx+8与y轴交于点C,
∴C(0,8),
∵OC=2OB,
∴B(4,0)
∵抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,
∴
,
解得
.
∴抛物线的解析式为y=-x2+2x+8;
(2)设BC的中点为E,
∵B(4,0),C(0,8),
∴E(2,4),
设直线OE的解析式为y=kx,
∴4=2k,解得k=2,
∴直线OE的解析式为y=2x,
∴
,
解得
或
.
∴N的坐标为(2
,4
)或(-2
,-4
).
∴C(0,8),
∵OC=2OB,
∴B(4,0)
∵抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,
∴
|
解得
|
∴抛物线的解析式为y=-x2+2x+8;
(2)设BC的中点为E,
∵B(4,0),C(0,8),
∴E(2,4),
设直线OE的解析式为y=kx,
∴4=2k,解得k=2,
∴直线OE的解析式为y=2x,
∴
|
解得
|
|
∴N的坐标为(2
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了待定系数法求解析式,以及二次函数图象上点的坐标特征,关键是求得BC的中点坐标,进而求得经过中点和原点的直线.

练习册系列答案
相关题目
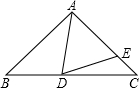 如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上,AD=AE,∠BAD=30°.
如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上,AD=AE,∠BAD=30°.