题目内容
在平行四边行ABCD中,BC=2AB,将AB向两端延长,使AE=AB=BF,且EC,FD相交于点G,求证:∠EGF=90°.
考点:平行四边形的性质
专题:
分析:连接MN,求出DM=DC=CN,根据菱形的判定推出四边形CNMD是菱形,根据菱形的性质得出即可.
解答: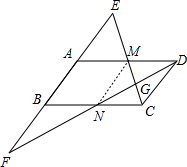 证明:连接MN,
证明:连接MN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,AB∥CD,
∴△AEM∽△DCM,
∴
=
,
∵AB=AE=BF,AB=CD,
∴AE=CD,
∴AM=DM,
∵AD=2AB,AB=CD,
∴DM=DC,
同理CN=DC,
∴DM∥CN,DM=CN,
∴四边形CNMD是菱形,
∴FD⊥EC,
故∠EGF=90°.
 证明:连接MN,
证明:连接MN,∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,AB∥CD,
∴△AEM∽△DCM,
∴
| AE |
| CD |
| AM |
| DM |
∵AB=AE=BF,AB=CD,
∴AE=CD,
∴AM=DM,
∵AD=2AB,AB=CD,
∴DM=DC,
同理CN=DC,
∴DM∥CN,DM=CN,
∴四边形CNMD是菱形,
∴FD⊥EC,
故∠EGF=90°.
点评:本题考查了平行四边形的性质,菱形的性质和判定,相似三角形的性质和判定的应用,注意:菱形的对角线互相垂直.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
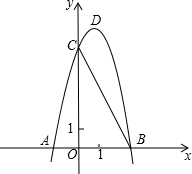 如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求
如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求