题目内容
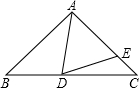 如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上,AD=AE,∠BAD=30°.
如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上,AD=AE,∠BAD=30°.(1)求∠EDC的度数;
(2)若∠B=30°,请判断△ADE的形状,并写出证明过程;
(3)若∠B=45°,请判断△ADE的形状,直接写出结论,不必写出写出证明过程.
考点:等腰三角形的判定与性质
专题:
分析:(1)设∠EDC=x,∠B=∠C=y,根据∠ADE=∠AED=x+y,∠ADC=∠B+∠BAD即可列出方程,从而求解.
(2)根据外角的性质求得∠ADC=60°,进而求得∠ADE=∠AED=45°,从而证得△ADE是等腰直角三角形;
(3)根据外角的性质求得∠ADC=75°,进而求得∠ADE=∠AED=60°,从而证得△ADE是等边三角形.
(2)根据外角的性质求得∠ADC=60°,进而求得∠ADE=∠AED=45°,从而证得△ADE是等腰直角三角形;
(3)根据外角的性质求得∠ADC=75°,进而求得∠ADE=∠AED=60°,从而证得△ADE是等边三角形.
解答:解:(1)设∠EDC=x,∠B=∠C=y,
∠AED=∠EDC+∠C=x+y,
又∵AD=AE,
∴∠ADE=∠AED=x+y,
则∠ADC=∠ADE+∠EDC=2x+y,
又∵∠ADC=∠B+∠BAD,
∴2x+y=y+30,
解得x=15,
∴∠EDC的度数是15°.
(2)△ADE是等腰直角三角形;
∵∠BAD=30°,∠B=30°,
∴∠ADC=60°,
∵∠EDC=15°,
∴∠ADE=45°,
∵AD=AE,
∴∠AED=45°,
∴△ADE是等腰直角三角形;
(3)△ADE是等边三角形;
∵∠BAD=30°,∠B=45°,
∴∠ADC=75°,
∵∠EDC=15°,
∴∠ADE=60°,
∵AD=AE,
∴∠AED=60°,
∴△ADE是等边三角形;
∠AED=∠EDC+∠C=x+y,
又∵AD=AE,
∴∠ADE=∠AED=x+y,
则∠ADC=∠ADE+∠EDC=2x+y,
又∵∠ADC=∠B+∠BAD,
∴2x+y=y+30,
解得x=15,
∴∠EDC的度数是15°.
(2)△ADE是等腰直角三角形;
∵∠BAD=30°,∠B=30°,
∴∠ADC=60°,
∵∠EDC=15°,
∴∠ADE=45°,
∵AD=AE,
∴∠AED=45°,
∴△ADE是等腰直角三角形;
(3)△ADE是等边三角形;
∵∠BAD=30°,∠B=45°,
∴∠ADC=75°,
∵∠EDC=15°,
∴∠ADE=60°,
∵AD=AE,
∴∠AED=60°,
∴△ADE是等边三角形;
点评:本题主要考查了等腰三角形的判定和性质,等边对等角,等角对等边;(1)正确确定相等关系列出方程是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
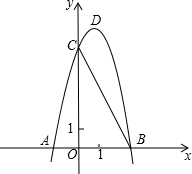 如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求
如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求